Students must start practicing the questions from CBSE Sample Papers for Class 12 Applied Mathematics with Solutions Set 10 are designed as per the revised syllabus.
CBSE Sample Papers for Class 12 Applied Mathematics Set 10 with Solutions
Maximum Marks: 80 Marks
Time Allowed : 3 Hours
General Instructions:
- This question paper contains five sections A, B, C, D and E. Each section is compulsory.
- Section – A carries 20 marks weightage, Section – B carries 10 marks weightage, Section – C carries 18 marks weightage, Section – D carries 20 marks weightage and Section – E carries 3 case-based with total weightage of 12 marks.
- Section A: It comprises of 20 MCQs of 1 mark each.
- Section B: It comprises of 5 VSA type questions of 2 marks each.
- Section C: It comprises of 6 SA type of questions of 3 marks each.
- Section D: It comprises of 4 LA type of questions of 5 marks each.
- Section E: It has 3 case studies. Each case study comprises of 3 case-based questions, where 2 VSA type questions are of 1 mark each and 1 SA type question is of 2 marks. Internal choice is provided in 2 marks question in each case-study.
- Internal choice is provided in 2 questions in Section – B, 2 questions in Section – C, 2 questions in Section – D. You have to attempt only one of the alternatives in all such questions.
Section – A [20 marks]
(All questions are compulsory. No internal choice is provided in this section
Question 1.
*The comer points of the feasible region determined by the following system of linear inequalities are (0,0), (5, 0), (3, 4) and (0, 5):
2x + y ≤ 10, x + 3y ≤ 15, x, y ≥ 0
Let Z = px+ qy, where p, q > 0
Condition on p and q so that the maximum of Z occurs at both (3, 4) and (0, 5) is:
(a) P = q
(b) p = 2q
(c) p = 3q
(d) q = 3p [1]
Answer:
(d) q = 3p
Explanation: Let the maximum value of Z be M. Then,
At (3, 4), M = 3p + 4q ….. (i)
At (0, 5), M = 5q ….. (ii)
From (i) and (ii), we have
3p + 4q = 5q
⇒ 3p = q
Question 2.
Mrs. Malhotra has decided to set up a sinking fund for the purpose of buying a computer in two years. It is expected that the computer will cost ₹ 20,000 at the end of 2 years. The size of equal quarterly installment she has to pay into the fund, if money’s worth 10% p.a. compounded quarterly, is
(a) ₹ 2290
(b) ₹ 2280
(c) ₹ 2350
(d) ₹ 3290 [1]
Answer:
(a) 2290
Explanation:
Here,
i = \(\frac{r}{4}\) = 0.025 ; A = ₹ 20,000 and n = 2 × 4 = 8
Let R be the quarterly installment, then, using the formula R = \(\frac{\mathrm{Ai}}{(1+i)^n-1}\)
we get R = 2290 (approx..)
So, (a) is the correct option
![]()
Question 3.
Present value of annuity of periodic dividend payments of R for n periods is given by
(a) R[1 – (1 + i)-n
(b) \(R\left[\frac{1-(1+i)^{-n}}{i}\right]\)
(c) R[1 – (1 + i)-n]
(d) R\(\left[\frac{1-(1+i)^n}{i}\right]\) [1]
Answer:
(b) R\(\left[\frac{1-(1+i)^{-n}}{i}\right]\)
Question 4.
A fire in a factory delaying production for some time is
(a) seasonal trend
(b) cyclical trend
(c) long term trend
(d) irregular trend [1]
Answer:
(d) irregular trend
Question 5.
A specific characteristic of a sample is called
(a) variance
(b) statistic
(c) parameter
(d) population [1]
Answer:
(b) statistic
Question 6.
For two independent samples X and Y (from two different populations), the statistic for t- test is:
 [1]
[1]
Answer:
(c) \(\frac{\bar{X}-\bar{Y}}{s \sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}\)
![]()
Question 7.
The marks obtained were found normally distribution with mean 75 and variance 100. The percentage of students who scored more than 75 marks is
(a) 25%
(b) 50%
(c) 75%
(d) 100% [1]
Answer:
(b) 50%
Explanation: Here,
Z = \(\frac{X-75}{10}\)
Thus, P( X > 75) = P(Z > 0) = 0.5
Hence, the percentage of students who scored more than 75 marks is 50%.
So, (b) is the correct option
Question 8.
For a fish merchant, the probability of getting daily profit of ₹ 1500 is 0.6, the probability of getting a loss of ₹ 1000 is 0.3 and the probability of getting neither profit nor loss is 0.1. Then, the mean daily profit of the fish merchant is
(a) ₹ 500
(b) ₹ 900
(c) ₹ 400
(d) ₹ 600 [1]
Answer:
(d) ₹ 600
Explanation: The possible outcomes, their probabilities and the corresponding values of gains(x) are shown below:
| Outcome | Probability(p) | Gain (x) | x. p. |
| Profit | 0.6 | 1500 | 900 |
| Loss | 0.3 | 1000 | -300 |
| No profit nor loss | 0.1 | 0 | 0 |
E(X) = \(\sum_{i=1}^n x_i p_i\) = 900 – 300 + 0 = 600
So, the correct option is (d)
Question 9.
Which of the following differential equations has y = c1ex + c2e-x as the general solution?
(a) \(\frac{d^2 y}{d x^2}\) + y = 0
(b) \(\frac{d^2 y}{d x^2}\) – y = 0
(c) \(\frac{d^2 y}{d x^2}\) + 1 = 0
(d) \(\frac{d^2 y}{d x^2}\) – 1 = 0
Answer:
(b) \(\frac{d^2 y}{d x^2}\) – y = 0
Explanation: On differentiating the given equation y = c1ex c2e-x, we have \(\frac{d y}{d x}\), c1ex – c2e-x
On differentiating once again,
we have \(\frac{d^2 y}{d x^2}\) = c1ex – c2e-x = y
⇒ \(\frac{d^2 y}{d x^2}\) – y = 0
Hence, (b) is the correct option.
Question 10.
If \(\frac{d}{d x}\)f(x) = 4x3 – \(\frac{3}{x^4}\) such that f(2) = 0. Then, f(x) is
(a) x4 + \(\frac{1}{x^3}\) – \(\frac{129}{8}\)
(b) x3 + \(\frac{1}{x^4}\) + \(\frac{129}{8}\)
(c) x4 + \(\frac{1}{x^3}\) + \(\frac{129}{8}\)
(a) x3 + \(\frac{1}{x^4}\) + \(\frac{129}{8}\) [1]
Answer:
(a) x4 + \(\frac{1}{x^3}\) – \(\frac{129}{8}\)
Explanation: Here, \(\frac{d}{d x}\)
f(x) = 4x3 – \(\frac{3}{x^4}\)
Integrating both sides, we have
f(x) = \(\int\left(4 x^3-\frac{3}{x^4}\right) d x\)
= \(\int 4 x^3 d x-\int \frac{3}{x^4} d x\)
= \(4 \int x^3 d x-3 \int x^{-4} d x\)
= x4 + x-3 + C
Since f(2) = 0, we have (2)4 + (2)-3 + C = 0
⇒ C = \(-\frac{129}{8}\)
Hence, f(x) = x4 + \(\frac{1}{x^3}\) – \(\frac{129}{8}\)
Question 11.
Let x be a number which exceeds its square by the greatest possible quantity. Then, x is equal to
(a) \(\frac{1}{2}\)
(b) \(\frac{1}{4}\)
(c) \(\frac{3}{4}\)
(d) \(\frac{1}{3}\)
Answer:
(a) \(\frac{1}{2}\)
Explanation:
Let
f(x) = x – x2. Then, f'(x) = 1 – 2x and f “(x) = -2
f'(x) = 0 implies 1 – 2x = 0, or x = \(\frac{1}{2}\)
i.e., x = \(\frac{1}{2}\) is a critical point.
Now, f”(\(\frac{1}{2}\)) = -2 < 0 So, f'(x) is maximum when x = \(\frac{1}{2}\)
Thus, (a) is the correct option
Question 12.
The matrix \(\left[\begin{array}{lll} 0 & 0 & 5 \\ 0 & 5 & 0 \\ 5 & 0 & 0 \end{array}\right]\) is a
(a) scalar matrix
(b) diagonal matrix
(c) unit matrix
(d) square matrix [1]
Answer:
(d) square matrix Explanation: It is simply a square matrix.
Question 13.
If \(\left[\begin{array}{ll} 1 & 2 \\ 2 & 1 \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right]\) = \(\left[\begin{array}{l} 5 \\ 4 \end{array}\right]\), then(x + y) equals
(a) 3
(b) 5
(c) 2
(d) 7 [1]
Answer:
(a) 3
Explanation:

x + 2y = 5 and 2x + y = 4 x + y = 3
Question 14.
If the matrix P = \(\left[\begin{array}{cc} 2 & 3 \\ 5 & -1 \end{array}\right]\) = A + B, where A is a symmetric and B is skew – symmetric matrices, then B equals

Answer:
(d) \(\left[\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\right]\)
Explanation: Here, B = \(\frac{1}{2}\left[P-P^{\top}\right]\)

![]()
Question 15.
The linear inequality representing the solution set given in the figure below is:
![]()
(a) |x| > 3
(b) |x| < 3
(c) |x| ≥ 3
(d) |x| ≤ 3
Answer:
(c) |x| ≥ 3
Explanation: The solution set represented on the number line is [3, ∞) ∪ (-∞, -3]. which is equivalent to |x| ≥ 3.
Question 16.
If \(\frac{|x-5|}{x-5}\) ≤ 0, then
(a) x ∈ [5, ∞)
(b) x ∈ [-∞, 5)
(C) x ∈ (5, ∞)
(D) x ∈ (-∞, 5)
Answer:
(b) x ∈ [-∞, 5)
Explanation: Since,

Question 17.
In a 500 m race, the ratio of the speeds of A and B is 3:4. A has a start of 140 m. By how many metres A wins?
(a) 18 m
(b) 20 m
(c) 22 m
(d) 26 m [1]
Answer:
(b) 20 m
Explanation: To reach the winning post, A has to cover a distance of (500 – 140) = 360 m
Since the speeds of A and B is 3 : 4.
when A covers 360 m, B covers ₹ = 480 m
Therefore, A wins by (500 – 480) = 20 m
Question 18.
Two pipes A and B can fill a tank in 40 minutes and 30 minutes respectively. If both the pipes are opened simultaneously, then how much time will be taken to fill the tank?
(a) 17′ minutes
(b) 17′ minutes
(c) 16′ minutes
(d) 18 minutes [1]
Answer:
(a) 17’ minutes
Assertion-Reason Questions
Two statements are given-one labelled Assertion (A) and the other labelled Reason (R). Select the correct answer to these questions from the codes (a), (b), (c) and (d) as given below:
(a) Both (A) and (R) are true and (R) is the correct explanation of (A).
(b) Both (A) and (R) are true but (R) is not the correct explanation of (A).
(c) (A) is true but (R) is false.
(d) (A) is false but (R) is true
Question 19.
Assertion (A): Minor of element of in the matrix \(\left[\begin{array}{ccc}
0 & 2 & 6 \\
1 & 2 & -1 \\
2 & 1 & 3
\end{array}\right]\) is -3
Reason (R): Minor of an element aij of a matrix is the determinant obtained by deleting its ith row. [1]
Answer:
(c) (A) is true but (R) is false
Explanation:
M13 \(\left[\begin{array}{ll}
1 & 2 \\
2 & 1
\end{array}\right]\) = 1 – 4 = -3
So given assertion is true. The minor of an element aji of a matrix is the determinant obtained by deleting its ith row and jth column. So, reason is false.
Question 20.
Assertion (A) : The third derivative of y = logx is \(-\frac{2}{x^3}\)
Reason (R) : The differentiation process could be continued to find the third, fourth and successive derivatives of f(x), which are called higher order derivative of f(x).
Answer:
(d) (A)is false but (R) is true.
Explanation:
Given: y = log x,
\(\frac{d y}{d x}\) = \(\frac{1}{x}\)
\(\frac{d^2 y}{d x^2}\) = \(-\frac{1}{x^2}\)
and \(\frac{d^3 y}{d x^3}\) = \(\frac{2}{x^3}\)
Section – B
(All questions are compulsory. In case of internal choice, attempt any one question only)
Question 21.
A man can row 6 km/h in still water. It takes him twice as long to row up as to row down the river. Find the speed of the stream. [2]
Answer:
Let the speed of the stream be y km/h. Let the distance be ‘d’ km. Then,
d/(6 – y) = 2x d/(6 + y)
y = 2
So, the speed of the stream is 2 km/h
![]()
Question 22.
If -2\(\frac{1}{2}\) ≤ \(\frac{x}{2}\) – 1\(\frac{1}{3}\) < \(\frac{1}{6}\), then find the values of x when
(A) x is an integer (B) x is a natural number. [2]
Answer:
We have
-2\(\frac{1}{2}\) < \(\frac{x}{2}\) – 1\(\frac{1}{3}\) < \(\frac{1}{6}\)
-1\(\frac{1}{3}\) – 2\(\frac{1}{2}\) ≤ \(\frac{x}{2}\) < \(\frac{1}{6}\) + 1\(\frac{1}{3}\)
–\(\frac{7}{3}\) ≤ x < 3
(A) Solution set = {-2, -, 0, 1, 2}
(B) Solution set = {1, 2}
Question 23.
A country produces only two goods X and Y. The technology matrix is \(\left[\begin{array}{ll}
0.3 & 0.6 \\
0.5 & 0.1
\end{array}\right]\)
The final demand for X is 10 and for y is 5. Write down the input-out model as a set of simultaneous linear equations.
OR
Using inverse coefficient matrix, solve the system of equations:
{2x – y = 17
3x + 5y = 6 [2]
Answer:
Let X = \(\left[\begin{array}{l}
x_1 \\
x_2
\end{array}\right]\) be the gross output matrix required to meet the final demand D = \(\left[\begin{array}{c}
10 \\
5
\end{array}\right]\)
It is given that the technology matrix is
A = \(\left[\begin{array}{c}
10 \\
5
\end{array}\right]\)
Since production equals consumption, the balancing equations are:
0.3x1 + 0.6x2 + 10 = x1 and 0.5x1 + 0.1x2 + 5 = x2
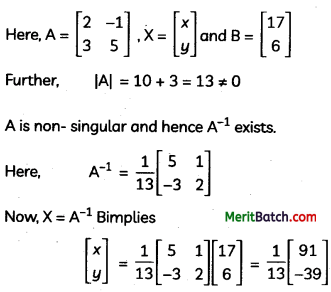
x = \(\frac{91}{93}\) = 7, y = –\(\frac{39}{13}\) = -3 is the required solution of the given system of equations
![]()
Question 24.
If y = 7x – x3 and x increases at the rate of 4 units per second, how fast is the slope of the curve changing , when x = 2?
OR
Find: \(\int \frac{x}{\sqrt{2 x^2+3}} d x\)
[2]
Answer:
Given y = 7x – x3, we have \(\frac{d y}{d x}\)(m) = 7 – 3x2
⇒ \(\frac{d m}{d x}\) = -6x ….(1)
It is given that \(\frac{d x}{d t}\) = 4. We need to find \(\left(\frac{d m}{d t}\right)_{x=2}\)
From (1), we obtain \(\frac{d m}{d t}\) = \(\frac{d m}{d x}\) × \(\frac{d x}{d t}\) = (-6x)(4)
= -24x
\(\left(\frac{d m}{d t}\right)_{x=2}\) = -24(2) = -48
Thus, the slope of the curve is decreasing at the rate of 48 units per second.
OR
\(\int \frac{x}{\sqrt{2 x^2+3}} d x\)
Put 2x2 + 3 = t so that 4x dx = dt
or x dx = \(\frac{1}{4}\) dt
so, \(\int \frac{x}{\sqrt{2 x^2+3}}\)dx = \(\frac{1}{4} \int \frac{1}{\sqrt{t}} d t\)
= \(\frac{1}{4} \cdot 2 \sqrt{t}+C\) = \(\frac{\sqrt{2 x^2+3}}{2}\) + C
Question 25.
Amrit Singh will receive ₹ 10,000 at the end of the 4th year. Calculate the present value if the discount rate is 12% and discounting is done quarterly. (Given (1.03)-16 = 0.623) [2]
Answer:
Le P denote the present value of the amount A = ₹10,000. Then,
P = \(\mathrm{A}\left(1+\frac{r}{m}\right)^{-n m}\)
gives P = 10,000\(\left(1+\frac{0.12}{4}\right)^{-4 \times 4}\)
= 10,000(1.03)-16
= 10,000 × 0.623 = ₹6230
Section – C [18 marks]
(All questions are compulsory. In case of internal choice, attempt any one question only)
Question 26.
A man borrows ₹ 10,00, 000 and agrees to pay interest quarterly at an annual rate of interest of 8%. At the same time, he sets up a sinking fund in order to repay the loan at the end of 5 years. If the sinking fund earns interest @ 6% per annum, compounded quarterly, find the quarterly cost of the debt. {Given (1.015)20 = 1.346852} [3]
Answer:
Here, the amount borrowed = 10,00,000;
Rate of interest = 8% = 0.08.
So, quarterly interest payment on the loan
= ₹(10,00,000 × 0.02) = ₹ 20,000
Amount S to be accumulated in the sinking fund
= ₹10,00,000
Rate of interest = 6% = 0.06; and n = 5 years = 20 quarters
Since interest is compounded quarterly,
r = \(\frac{0.06}{4}\) = 0.015
Let ₹ A be the quarterly installment payable in the sinking fund. Then,

Thus, the quarterly cost of the debt is ₹ 43,246 + ₹ 20,000, i.e ₹ 63,246.
Question 27.
Mr. X plans to set his son for higher studies abroad for 10 years. He expects the cost of the studies to be ₹ 2,00,000. How much must he set aside at the end of each quarter for 10 years to accumulate this amount, if money is worth 6% compounded annually. [Given (1.015)40 = 1.8140] [3]
Answer:
Here, A = x (say), r = \(\frac{6}{400}\) = 0.015 and n = 10 × 4=40
So, S = \(\frac{A}{r}\)[(1 + r)n – 1] gives
2,00,000 = \(\frac{x}{0.015}\)[(1.015)40 – 1]
⇒ S = \(\frac{3000}{[1.8140-1]}\)
= \(\frac{3000}{0.8140}\) = 3685.50
Thus, Mr.X should set aside a sum ₹3685.50
![]()
Question 28.
Solve the following LPP graphically using corner point method:
Maximise Z = 5x + 3y subject to the constraints
3x + 5y < 15; 5x + 2y ≤ 10
x ≥ 0, y ≥ 0. [3]
Answer:
Here, the graph of the given constraints and the feasible region, so obtained, is shaded in the graph given below:

| Corner point |
Corresponding value of Z |
| O(0, 0) | 5(0) + 3(0) = 0 |
| A(2, 0) | 5(2) + 3(0) = 10 |
| B(\( \frac{20}{19} \), \( \frac{45}{19} \)) | 5(\( \frac{20}{19} \)) + 3(\( \frac{45}{19} \)) = \( \frac{235}{19} \) = 12\( \frac{7}{19} \)) |
| C(0, 3) | 5(0) + 3(3) = 9 |
Thus, maximum value of z is 12\(\frac{7}{19}\) which occurs at B(\(\frac{20}{19}\), \(\frac{45}{19}\))
Question 29.
Three pipes A, B and C can fill a tank together in 8 hours. After working at it together for 2 hours B is closed and A and C can fill the remaining part of the tank in 9 hours. Find the time in which B alone can fill the tank. [3]
Answer:
Part of the tank that will be filled by three pipes together in 2 hours = 2/8 = 1/4
Remaining part of the tank = 1 – 1/4= 3/4 In 9 hours, A and C can fill 3/4 of the tank.
So, in 1 hour, A and C can fill (3/4 × 1/9 ), i.e., 1/12 of the tank Further,
Part of the tank that will be filled by three pipes together in 1 hour = 1/8
Part of the tank that will be filled by B alone = 1/8 – 1/12 = 1/24
So, B alone can fill the tank in 24 hours.
Question 30.
X is a discrete random variable having the following probability distribution:
| Xi | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P(X = xi) | 0 | K | 2k | 2k | 3k | k2 | 2k2 | 7k2 + k |
(A) Determine the constant k
(B) Find P(X < 6)
(C) Find P(X3 ≥ 6)
OR
A box contains 4 white and 6 black balls. If 3 balls are drawn at random, find the mathematical expectation of the number of white balls. [3]
Answer:
Since Σ(X = xi) = 1
0 + k + 2k + 2k + 3k + k2 + 2k2 + 7k2 + k = 1
(A) 9k + 10k2 = 1(10k – 1)(k + 1) = 0
⇒ k = \(\frac{1}{10}\) {k ≠ -1}
(B) P(X < 6) = 1 – {P(X = 6) + P(X = 7)}
= 1 – \(\left\{\frac{2}{100}+\frac{17}{100}\right\}\)
= \(\frac{81}{100}\), or 0.81
(C) P(X ≥ 6) = P(X = 6) + P(X = 7)
= \(\frac{2}{100}\) + \(\frac{17}{100}\) = \(\frac{19}{100}\) or 0.19
OR
Here the variable X is the number of white balls obtained among the 3 balls drawn. Then X takes values 0, 1, 2, 3
P(X = 0) = P(0 white ball)

= 0 + \(\frac{1}{2}\) + \(\frac{3}{5}\) + \(\frac{1}{10}\) = \(\frac{6}{5}\), or 1.2
![]()
Question 31.
A sample size of 10 drawn from a normal population has a mean 31 and a variance 2.25. Is it reasonable to assume that the mean of the population is 30? [ Use 1% level of significance, given that (t9 (0.1) = 3.25)
OR
Certain medicine is packed into bags by a machine. A random sample of 10 bags drawn and their contents are found to weigh (in kg) as follows:
40, 45, 48, 50, 52, 55, 45, 52, 63, 40
Test if the average packing can be taken to be 50 kg (Given t9 (0.05) = 2.26) [3]
Answer:
Ho : μ = 30, s = 1.05, n = 10 and \(\overline{\mathrm{X}}\) = 31
To test H0, the statistic t is
t = \(\frac{\bar{X}-\mu}{s / \sqrt{n-1}}\) = \(\frac{31-30}{1.5 / \sqrt{9}}\) = 2
The table value of t at a = 0.01 and 9 d.f. is 3.25
Conclusion: Since |t| < t∝, the null hypothesis is accepted. i.e., sample can be regarded from the assumed population ∝ = 0.01
OR
Here, H0 : μ = 50, i.e., there is no significant difference between the sample mean and population mean.
H1 : μ ≠ 50

Applying t-test,
t = \(\frac{\overline{\mathrm{X}}-\mu}{\mathrm{S} / \sqrt{n}}\)
= \(\frac{49-50}{\sqrt{49.56 / 10}}\) = -0.45
⇒ |t| = 0.45
Tabulated to.05 for (10 – 1), i.e., 9 d.f. is 2.26
Conclusion: Since |t| < t0.05, the null hypothesis is accepted at 5% level of significance and we may conclude that the data are consistent with the average packing of 50 kg.
Section – D (20 marks)
(All questions are compulsory. In case of internal choice, attempt any one question only)
Question 32.
Given the following data from two independent samples:
| Sample 1 | Sample 2 |
| Sample mean (\( \bar{X} \)) = 25.8
S.D. (s1) = 12.6 n1 = 15 |
Sample mean (\( \bar{Y} \)) = 28.4
S.D. (s2) = 28.2 n1 = 12 |
Test the significance of difference between two means. (Given t25 (0.05) = 2.06) [5]
Answer:

Tabulated t0.05 for (15 + 12 – 2), i.e 25 d.f. for two-tailed test is 2.06
Conclusion: Since |t| < tα, the null hypothesis is accepted, i.e., there is no significant difference between the two means.
Question 33.
The rate of growth of a population is proportional to the number present, If the population of a city doubled in the past 25 years and the present population is 1,00,000, when will the city have a population of 5,00,000?
OR
Evaluate: \(\int_0^1 \frac{e^{-x}}{1+e^x} d x\) [5]
Answer:
Let P(t) be the population of a city at any time t Then,
\(\frac{d \mathrm{P}}{d t}\) = kP, where k is constant of proportionality.
⇒ \(\frac{d \mathrm{P}}{p}\) = k dt
Integrating both sides, we have = \(\int \frac{d P}{P}\) = \(\int k d t\)
Log P = kt + C … (1)
Let P0 be the initial population at t = 0.
Then , from (1), C = log Po
∴ From (1), we get log \(\left(\frac{P}{P_0}\right)\) = kt … (2)
Now P = 2P0 when t = 25. So, by (2),
we have log\(\left(\frac{2 \mathrm{P}_0}{\mathrm{P}_0}\right)\) = 25k, or k = \(\frac{1}{25}\) log 2
From (2), we have log\(\left(\frac{5,00,000}{1.00 .000}\right)\) = \(\frac{1}{25}\)log 2.t,
or log (5) = \(\frac{1}{25}\)log 2. t
t = 25\(\frac{\log 5}{\log 2}\) = 25 × \(\frac{1.609}{0.6931}\)
= 58 (approx.)
Thus, the city will, have a population of 5,00,000 in 58 years.
OR
Let I = \(\int_0^1 \frac{e^{-x}}{1+e^x} d x\)
= \(\int_0^1 \frac{1}{e^x\left(1+e^x\right)} d x\)
Put ex = t so that exdx = dt or dx = \(\frac{d t}{t\left(=e^x\right)}\)
When x = 0, t = 1 and when x = 1, t = e

Comparing the coeffcients of t2, t and the constant, we have
A + C = 0; A + B = 0 ; B = 1
Solving these equations, we get A = -1, B = 1, C = 1
Thus, from (1), we have

![]()
Question 34.
Taking 2002 as the base year, with an index number 100, calculate index number for 2005, based on weighted average of price relatives derived from the table given below:
| Commodity | A | B | C | D |
| Weight | 30 | 15 | 25 | 30 |
| Price(in ₹) in 2002 | 20 | 10 | 5 | 40 |
| Price(in ₹) in 2005 | 24 | 20 | 30 | 40 |
The weights are now changed so that the weight for A is 40 and C is 10 and total weight is 100. If the value of index number in 2005 with the changed weight is 175, calculate the weights applied to B and D.
OR
For the following data, fit a straight line trend by method of least squares. Tabulate the trend values and also,, estimate the most likely sales for the year 2007.
| Year | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 |
| Sales(₹ lakhs) | 10 | 20 | 30 | 56 | 40 | 60 |
Answer:
We have the following table:

Here ΣPw = 24600 and Σw = 100
So, index number = \(\frac{\sum^{P w}}{\sum^w}\) = \(\frac{26400}{100}\) = 246
Again, construct the following table.

Here, ΣPw = 15800 + 1oox and Σw = 100
So, index number = \(\frac{\sum^{P w}}{\sum^w}\) = \(\frac{15800+100 x}{100}\)
= 158 + x
Equating it to 175,
we have 175 = 158 + x
⇒ x = 17
Hence, the weights applied to B and D are 17 and 33, respectively.
OR
Here, n = 6(Even).
Let the equation of the straight line of best fit, with the origin at the mid of the years 2003 and 2004 and units of x as \(\frac{1}{2}\) year, be y = a + bx
By the method of least squares, the values of ‘a’ and ‘b’ are given by
a = \(\frac{\Sigma y}{n}\) and b = \(\frac{\Sigma x y}{\Sigma x^2}\) … (A)
Calculation for fitting the line of best fit
| Year | Value | x | x2 | xy |
| 2001 | 10 | -5 | 25 | -50 |
| 2002 | 20 | -3 | 9 | -60 |
| 2003 | 30 | -1 | 1 | -30 |
| 2004 | 56 | 1 | 1 | 56 |
| 2005 | 40 | 3 | 9 | 120 |
| 2006 | 60 | 5 | 25 | 300 |
| Σy = 216 | Σx = 0 | Σx2 = 70 | Σxy = 336 |
Using (A), we have

Hence, the required equation of the best fitted straight line is y = 36 + 4.8 x
| Year | x | Trending value (y = 36 + 4.8x) |
| 2001 | -5 | 36 + 4.8(-5) = 12 |
| 2002 | -3 | 36 + (4.8)(-3) = 21.6 |
| 2003 | -1 | 36 + 4.8(-1) = 31.2 |
| 2004 | 1 | 36 + 4.8(1) = 40.8 |
| 2005 | 3 | 36 + 4.8(3) = 50.4 |
| 2006 | 5 | 36 + 4.8(5) = 60 |
Thus, the trend values are 12, 21.6, 31.2, 40.8, 50.4 and 60
Estimate for the year 2007 = 36 +4.8(7) = 69.6
![]()
Question 35.
A zero coupon bond has ₹ 1000 face value with 25 years life. The appropriate rate of return is 9% p.a. What is the value of the zero coupon bond? Find out what should be the value of the bond after 10 years?
[Given (1.09)-25 = 0.11614 and (1.09)-10 = 0.42269) [5]
Answer:
Here,
F = Face value of the bond = 1000
n = number of periodic dividend payments = 25
i = Annual yield rate = 0.09
R = ₹ 0
Since the bond is to be redeemed at par,
C = Redemption price or Maturity value = Face value = ₹ 1000
Let V be the purchase value of the bond. Then,

= ₹ 1000(0.11614) = ₹116
The value V of the bond after 10 years is given by
V = ₹ 1000 (1.09)-10)}
= ₹ 1000 (0.42 269) = 422,69
Thus, the value V of the bond after 10 years is ₹ 42 2.69.
Section – E [12 marks]
(All questions are compulsory. In case of internal choice, attempt any one question only)
Question 36.
In number theory, it is after important to find factors of an integer number N. Any number N has four obvious factors ±1 and ±N. These are called ‘trivial factors’ Any other factor, if it exists, would be called ‘non-trivial’ Amar has platted a graph with points A (0, 50 Y, B (20, 40), C (50,100), D (0, 200) and E (100,0). [2]

This graph is constructed using three non trivial constraints and two trivial constraints one of the non-trivial constraints is x = 2y ≥ 0.
Based on the given information, answer the following question:
(A) What are the two trivial constraints. [1]
(B) If R2 is a feasible region, than what are the other two non-trivial constraints? [1]
(C) Given that the point (x, y) is in the region R1, then what is the maximum value of 5x + 2y?
OR
Given that the point (x, y) is in the region R2, than what is the maximum value of 5x + 2y. [2]
Answer:
(A) x ≥ 0, y ≥ 0
From the graph we can see that x and y is greater than or equal to.
(B) Region R2 is bounded by 2x – y = 0 and 2x + y = 200 and shaded region is towards origin. Then, constraints are 2x – y ≥ 0, 2x + y ≥ 200.
(C)Here Z = 5x + 2y
ZA = 5 × 0 + 2 × 50= 100
ZB = 5 × 20 + 2 × 40 = 180
ZC = 5 × 50 + 2 × 100 = 450
ZD = 5 × 0 + 2 × 200 = 400
∴ Maximum value of z is 450.
OR
For region R2, the corner points are B(20, 40), C (50, 100) and E (100, 0)
Here, Z = 5x + 2y
∴ ZB = 5 × 20 + 2 × 40
= 100 + 50
= 180
= 5 × 50 + 2 × 100
= 250 + 200
= 450
ZE = 5 × 100 + 2 × 0
= 500
Hence, the maximum value is 500 at point E (100, 0).
![]()
Question 37.
A trust is having a fund of ₹ 30,000 is to be invested into two different types of bonds. The first bond pays 5% interest P.O. which goes to an orphanage and second bond pays 7% interest p.a. which will be given to an NGO fighting for ‘acid attack survivors’. The trust wishes to divide ₹ 30,000 among two types of bond in such a way that they earn an annual total interest of ₹ 1800.

Based on the given Information, answer the following question:
(A) If amount invested in two bonds be x and y respectively, then form the system of equations for the given situation? [1]
(B) Write the system of equations in matrix forms. [1]
(C) What is the inverse of the matrix \(\left[\begin{array}{ll}
1 & 1 \\
5 & 7
\end{array}\right]\)
OR
What is the value of x and y in the given equations. [2]
Answer:
(A) ATQ
x + y = 30000
5% of x + 7% of y = 1800
5x + 7y = 180000
(B) The system of equations formed are
x + y = 30000
5x + 7y= 180000
In matrix forum,
\(\left[\begin{array}{ll}
1 & 1 \\
5 & 7
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{c}
30000 \\
180000
\end{array}\right]\)
(C)

OR
The equation in matric form is


∴ x = 15,000 and y = 15,000
Question 38.
The coordinated efforts of the local community and district administration have transformed the poor hygienean diseases driven village.

In continuation, to get rid of sewage and waste water, the local department wish to construct an underground septic tank with a square base which can hold a given quantity V of water and sludge with a metal sheet in minimum cost. Assume the side of the square be V and height of the tank be ‘h’
Based on the given information, answer the following question:
(A) What is the relation among x, h and V? [1]
(B) What is the surface area S(x) of the tank? [1]
(C) What will be the relation between x and h for which the cost of construction will be the least?
OR
If V = 13500, find the value of x? [2]
Answer:
(A) Here, V = x2h
⇒ h = \(\frac{V}{x^2}\)
This is the required relation.
(B) Here, S(x) = x2 + 4xh
⇒ S(x) = x2 + 4x\(\left(\frac{V}{x^2}\right)\)
= x2 + \(\frac{4 \mathrm{~V}}{x}\)
(C) For S(x) = x2 + \(\frac{4 \mathrm{~V}}{x}\), S’X = 2x – \(\frac{4 \mathrm{~V}}{x^2}\) and S”(x) = 2 + \(\frac{2 \mathrm{~V}}{x^3}\)
Now, S'(x) = 0 implies 2x – \(\frac{4 \mathrm{~V}}{x^2}\) = 0,
ie, x3 = 2V
s”(x) = 2 + \(\frac{2 \mathrm{~V}}{2 \mathrm{~V}}\) = 3 < 0
So, S(x) is least when x3 = 2V, or h = \(\frac{x}{2}\)
Thus, cost wilt be least when h = \(\frac{x}{2}\)
OR
From (A) h = \(\frac{\mathrm{V}}{x^2}\) and h = \(\frac{x}{2}\)
⇒ \(\frac{V}{x^2}\) = \(\frac{x}{2}\) or, x3 = 2V
For V = 13,500, x3 = 27,000
⇒ x = 30