CBSE Sample Papers for Class 12 Applied Mathematics Set 3 with Solutions

Students must start practicing the questions from CBSE Sample Papers for Class 12 Applied Mathematics with Solutions Set 3 are designed as per the revised syllabus.

CBSE Sample Papers for Class 12 Applied Mathematics Set 3 with Solutions

Maximum Marks: 80 Marks
Time Allowed : 3 Hours

General Instructions:

This question paper contains five sections A, B, C, D and E. Each section is compulsory.
Section – A carries 20 marks weightage, Section – B carries 10 marks weightage, Section – C carries 18 marks weightage, Section – D carries 20 marks weightage and Section – E carries 3 case-based with total weightage of 12 marks.
Section A: It comprises of 20 MCQs of 1 mark each.
Section B: It comprises of 5 VSA type questions of 2 marks each.
Section C: It comprises of 6 SA type of questions of 3 marks each.
Section D: It comprises of 4 LA type of questions of 5 marks each.
Section E: It has 3 case studies. Each case study comprises of 3 case-based questions, where 2 VSA type questions are of 1 mark each and 1 SA type question is of 2 marks. Internal choice is provided in 2 marks question in each case-study.
Internal choice is provided in 2 questions in Section – B, 2 questions in Section – C, 2 questions in Section – D. You have to attempt only one of the alternatives in all such questions.

Section – A (20 marks)

(All questions are compulsory. No internal choice is provided in this section)

Question 1.
Which one of the following is correct? [1]
(a) Every LPP admits an optimal solution
(b) A LPP admits a unique solution
(c) The optimal value occurs at a corner point of the feasible region
(d) If a LPP admits two optimal solutions, then it has infinite optimal solutions.
Solution:
(d) If a LPP admits two optimal solutions, then it has infinite optimal solutions.

Question 2.
Which of the following differential equations has y = x as the particular solution? [1]
(a) \(\frac{\mathrm{d}^{2} \mathrm{~y}}{\mathrm{dx}^{2}}\) -x²\(\frac{\mathrm{dy}}{\mathrm{dx}}\) + xy = x
(b) \(\frac{\mathrm{d}^{2} \mathrm{~y}}{\mathrm{dx}^{2}}\)+ x \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + xy = x
(c) \(\frac{\mathrm{d}^{2} \mathrm{~y}}{\mathrm{dx}^{2}}\) – x²\(\frac{\mathrm{dy}}{\mathrm{dx}}\) + xy = 0
(d) \(\frac{\mathrm{d}^{2} \mathrm{~y}}{\mathrm{dx}^{2}}\) + x \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = o
Solution:
(c) \(\frac{\mathrm{d}^{2} \mathrm{~y}}{\mathrm{dx}^{2}}\) – x²\(\frac{\mathrm{dy}}{\mathrm{dx}}\) + xy = 0

Explanation:
On differentiating the given equation y = x \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 1
On differentiating once again, we have \(\frac{\mathrm{d}^{2} \mathrm{~y}}{\mathrm{dx}^{2}}\) = 0
Equation \(\frac{\mathrm{d}^{2} \mathrm{~y}}{\mathrm{dx}^{2}}\) – x² \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + xy = 0 in (C) option is the only equation which is satisfied by these values of \(\frac{\mathrm{dy}}{\mathrm{dx}}\) and \(\frac{\mathrm{d}^{2} \mathrm{~y}}{\mathrm{dx}^{2}}\).
Hence, (c) is the correct option.

Question 3.
If ‘X’ is normally distributed with mean 30 and variance 25, then the standard normal variable Z corresponding to X = 32 is: [1]
(a) 0.08
(b) 0.48
(c) 0.44
(d) 0.4
Solution:
(d) 0.4

Explanation:
Here, Z = \(\frac{X-30}{5}\) Thus, for
X = 32,
Z = \(\frac{32-30}{5}\) = 0.4
So, (d) is the correct option

Question 4.
If one wants to measure changes in total monetary worth, then right choice should be: [1]
(a) a quantity index
(b) a value index
(c) a price index
(d) none of these
Solution:
(b) a value index

Question 5.
E(X) of the random variable X having the following distribution is: [1]
tableee
(a) 1
(b) 2
(c) \(\frac{1}{2}\)
(d) \(\frac{1}{3}\)
Solution:
(a) 1

Explanation:
E(X) = (0 × \(\frac{1}{2}\)) + (1 × \(\frac{1}{6}\)) + (2 × \(\frac{1}{6}\)) + (3 × \(\frac{1}{6}\))
= 0 + \(\frac{1}{6}\) + \(\frac{1}{3}\) + \(\frac{1}{2}\) = 1

Question 6.
Which index number is called ideal index number? [1]
(a) Laspeyre’s index
(b) Passche’s index
(c) Fisher’s index
(d) Dorbish and Bowley’s index
Solution:
(c) Fisher’s index

Question 7.
The recurrence formula for the poisson distribution is: [1]
(a) P(X = r + 1) = \(\frac{\lambda}{r+1}\) P(X = r)
(b) P(X = r + l) = \(\frac{\lambda}{r-1}\) P(X = r)
(c) P(X = r + 1) = \(\frac{\lambda}{r}\) P(X = r)
(d) P(X = r + l) = \(\frac{\lambda}{r(r+1)}\) P(X = r)
Solution:
(a) P(X = r + 1) = \(\frac{\lambda}{r+1}\) P(X = r)

Question 8.
If the mean of binomial distribution is 81, then standard deviation lies in the interval [1]
(a) [0, 9)
(b) (0, 9]
(c) [0, 3)
(d) (0, 3]
Solution:
(a) [0, 9)

Explanation:
Here, np = 81
So, variance = npq = 81q
⇒ 0 ≤ 81 q ≤ 81 ⇒ 0 ≤ \(\sqrt{81q}\) < 9
Hence, S.D ∈ [0, 9).

Question 9.
The function f(x) = a^x is strictly increasing on R, if [1]
(a) 0 < a < 1
(b) a < 0 (c) a > 0
(d) a > 1
Solution:
(d) a > 1

Explanation:
Given f(x) = a^x
So, f'(x) = a^x . Log a
Here, f'(x) > 0 if a > 0
Hence, fx) is strictly increasing when a >1

Question 10.
Under a settlement of property, Mr. Mahesh is entitled to receive ₹ 2400 per annum forever, the first being due at the end of first year. The present value of Mr. Mahesh’s right at 6% compounded annually is: [1]
(a) ₹ 24,000
(b) ₹ 34,000
(c) ₹ 40,000
(d) ₹48,000
Solution:
(c) ₹ 40,000
Explanation: Here, i = 0.06; R = ₹ 2400
Using P = \(\frac{\mathrm{R}}{\mathrm{i}}\), we get P = 40,000

Question 11.
A die is thrown once. Let X be the face number appeared. The mathematical expectation of X, is: [1]
(a) \(\frac{5}{2}\)
(b) \(\frac{7}{2}\)
(c) \(\frac{9}{2}\)
(d) \(\frac{3}{2}\)
Solution:
(b) \(\frac{7}{2}\)

Explanation:
E(X) = (1 × \(\frac{1}{6}\)) + (2 × \(\frac{1}{6}\)) + (3 × \(\frac{1}{6}\)) + (4 × \(\frac{1}{6}\)) + (5 × \(\frac{1}{6}\)) + (6 × \(\frac{1}{6}\))
= \(\frac{1}{6}\) (1 + 2 + 3 + 4 + 5 + 6)
= \(\frac{21}{6}\) = \(\frac{7}{2}\)

Question 12.
The order and degree of the differential equation: 1 + \(\left(\frac{d^2 y}{d x^2}\right)^2=\left[2+\left(\frac{d y}{d x}\right)^2\right]^{3 / 2}\) are respectively. [1]
(a) 2, 3
(b) 1, 2
(c) 2, 4
(d) 2, 2
Solution:
(c) 2, 4

Explanation:
The given differential equation can be simplified as [1 + (\(\frac{\mathrm{d}^{y} \mathrm{~s}}{\mathrm{dx}^{2}}\))²]² = [2 + (\(\frac{\mathrm{dy}}{\mathrm{dx}}\))²]³
The order of highest order derivative \(\frac{\mathrm{d}^{y} \mathrm{~s}}{\mathrm{dx}^{2}}\) is 2.
The power of the highest order derivative in the equation is 4.
Hence, (c) is the correct option.

Question 13.
What is present value of ₹ 10,000 receivable after 20 years if discounting rate is 8%? (Given (1.08)^-20 = 0.214) [1]
(a) 2000
(b) 2140
(c) 2040
(d) 3120
Solution:
(b) 2140

Explanation:
Let P denote the present value of the amount A = ₹ 10,000. Then,
P = A(1 + r)^{– n}
P = A(1.08)^-20
= 10,000 × 0.214 = ₹ 2140

Question 14.
If x + y ≤ 2, x, y ≥ 0, the point at which maximum value of 3x + 2y attained, will be : [1]

(a) (0, 2)
(b) (0, 0)
(c) (2, 0)
(d) (\(\frac{1}{2}\), \(\frac{1}{2}\))
Solution:
(c) (2, 0)

Explanation:
The corner points of the feasible region are : (2, 0), (0, 2) and (0, 0)
The values of Z at these corner points are 6, 4 and 0
Thus, Z_max = 6 at (2, 0)
So, the correct option is (c)

Question 15.
Arjun has an option to receive the value today for a debenture, face value ₹ 1000 carrying interest rate of 10% per annum. The debenture falls due for payment after three years. The present value today is: (Given (1.1)^-3 = 0.751) [1]
(a) 751
(b) 850
(c) 350
(d) 755
Solution:
(a) 751

Explanation:
Let P denote the present value of the amount A = ₹ 1000. Then,
P = A(1 + r)^{– n}
⇒ P = A(1 + 0.1)^-3
= 1000 × 0.751 = ₹ 751.

Question 16.
The present value of a perpetuity of ₹ 1000 payable at the end of each year, if money is worth 5% per annum, is: [1]
(a) 18,000
(b) 19,000
(c) 21,000
(d) 20,000
Solution:
(d) 20,000

Explanation:
Here, i = 0.05
Using the formula P_☐ = \(\frac{R}{i}\), we have
present value of a perpetuity of ₹ 1000
= ₹ \(\frac{1000}{0.05}\) = ₹ 20,000
Thus, the present value of a perpetuity is R 20,000.

Question 17.
The integrating factor of the differential equation (1 – y²)\(\frac{\mathrm{dx}}{\mathrm{dy}}\) + yx = ay(-1 < y < 1) is: [1]
(a) \(\frac{1}{y^2-1}\)
(b) \(\frac{1}{\sqrt{y^2-1}}\)
(c) \(\frac{1}{\sqrt{1-y^2}}\)
(d) \(\frac{1}{\sqrt{1+y^2}}\)
Solution:
(d) \(\frac{1}{\sqrt{1+y^2}}\)

Explanation:
Integrating factor = \(e^{\int \frac{y}{1-y^2} d y}\)
= \(e^{-\frac{1}{2} \log \left(1-y^2\right)}=e^{\log \left(\frac{1}{\left.\sqrt{1-y^2}\right)}\right.}=\frac{1}{\sqrt{1-y^2}}\)
Hence, (d) is the correct option.

Question 18.
The anti – derivative of \(\left(\sqrt{x}+\frac{1}{\sqrt{x}}\right)\) equals: [1]
(a) \(\frac{1}{3}\) x^1/3 + 2x^1/2 + C
(b) \(\frac{2}{3}\) x^2/3 + \(\frac{1}{2}\) x² + C
(c) \(\frac{2}{3}\) x^3/2 + 2x^1/2 + C
(d) \(\frac{3}{2}\)x^2/3 + \(\frac{1}{2}\)x^1/2 + C
Solution:
(c) \(\frac{2}{3}\) x^3/2 + 2x^1/2 + C

Explanation:

Assertion-Reason Questions

Two statements are given-one labelled Assertion (A) and the other labelled Reason (R). Select the correct answer to these questions from the codes (a), (b), (c) and (d) as given below:
(a) Both (A) and (R) are true and (R) is the correct explanation of (A).
(b) Both (A) and (R) are true but (R) is not the correct explanation of (A).
(c) (A) is true but (R) is false.
(d) (A) is false and (R) is true.

Question 19.
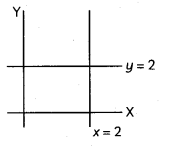
Assertion (A): The graph of x ≤ 2 and y ≥ 2 will be situated in the first and second quadrants. [1]
Reason (R):

Solution:
(a) Both (A) and (R) are true and (R) is the correct explanation of (A).

Explanation:
It is clear from the graph given in the reason (R) that assertion (A) true.

Question 20.
Assertion (A): If A and B are symmetric matrices, then AB – BA is a skew symmetric matrix [1]
Reason (R): (AB)’ = B’A’
Solution:
(a) Both (A) and (R) are true and (R) is the correct explanation of (A).

Explanation:
(AB)’ = B’A’
⇒ R is true.
Given that A and B are symmetric matrices
∴ A’ = A
and B’ = B
(AB – BA)’ = (AB) – (BA)’
⇒ B’ A’ – A’ B’ = BA – AB
since, (AB – BA)’ = – (AB -BA)
AB – BA is skew symmetric
Hence, A is true and R is the correct explanation of A.

Section – B (10 marks)

(All questions are compulsory. In case of internal choice, attempt any one question only)

Question 21.
Graph the following system of constraints and shade the feasible region: [2]
x – y ≤ 2; x + y ≤ 4
x ≥ 0, y ≥ 0
Solution:

Question 22.
A boat takes thrice as long as to go upstream to a point as to return downstream to the starting point. If the speed of the stream is 5 km/h, find the speed of the boat in still water. [2]
Solution:
Let the speed of the boat in still water be x km/h; and the speed of the stream be y km/h.
Here,
Speed of the downstream = x + y = 48/20 = 2.4
Speed of the upstream = x – y = 48/24 = 2
x = 2.2
Thus, the speed of the boat in still water be 2.2 km/h.

Question 23.
Using inverse coefficient matrix, solve the system of equations: 2x + 3y = 10; x + 6y = 4 [2]
OR
Using Cramer’s rule, show that the following system of equations has no solution:
2x – y + z = 4
x + 3y + 2z = 12
3x + 2y + 3z = 10
Solution:

x = \(\frac{48}{9}\) = \(\frac{16}{3}\), y = –\(\frac{2}{3}\) is the required solution of the given system of equations.

Here, D = \(\left|\begin{array}{ccc}
2 & -1 & 1 \\
1 & 3 & 2 \\
3 & 2 & 3
\end{array}\right|\)
= 2(9 – 4) + 1(3 – 6) + 1 (2 – 9) = 0;
D_x = \(\left|\begin{array}{ccc}
4 & -1 & 1 \\
12 & 3 & 2 \\
10 & 2 & 3
\end{array}\right|\)
= 4(9 – 4) + 1(36 – 20) + 1(24 – 30)
= 30 ≠ 0;
Since D = 0 and D_x ≠ 0 the system of equations has no solution.

Question 24.
Samples of sizes 10 and 14 were taken from two normal populations with S.D. 3.5 and 5.2. The sample means were found to be 20.3 and 18.6. Test whether the means of the two populations are the same at 5% level. [Given t₂₂ (0.05) = 2.07] [2]
Solution:
Let H₀ : µ₁ = µ₂, i.e., there is no significant difference between the two sample means.
H₁ : µ₁ ≠ µ₂ (two- tailed test)
Given \(\overline{\mathrm{X}}\) = 20.3, \(\overline{\mathrm{y}}\) = 18.6, n₁ = 10, n₂ = 14, s₁ = 3.5 , s₂ = 5.2

Tabulated t0.05 for (10 + 14 – 2), i.e., 22 d.f. for two – tailed test is 2.07
Conclusion: Since |t| < t_0.05, the null hypothesis is accepted at 5% level of significance.

Question 25.
In a 250 m race, the ratio of speeds of A and B is 1: 2. If A has a start of 140 m, then A wins by how many metres? [2]
OR
Solve for x: 2(2x + 3) -10 < 6(x -2).
Solution:
To reach the winning post, A has to cover a distance of ( 250 – 140) = 110 m
From the ratio given, when A covers 1 m, B covers 2 m
So, when A covers 110 m, B covers 220 m.
Thus, A wins by (250 – 220) = 30 m
OR
We have 2(2x + 3) -10 < 6(x -2)
4x + 6 < 6x – 12 2x > 18, or x > 9

Section – C (18 Marks)

(All questions are compulsory. In case of internal choice, attempt any one question only)

Question 26.
A pipe can empty a full tank in 40 minutes. A second pipe with diameter twice as much as the first is also attached with the tank to empty it. How much time will the two pipes together take to empty the tank? [3]
OR
If a > 0 and b> 0, prove that a³ + b³ ≥ a²b + ab².
Solution:
Let the diameters of the two pipes be ‘d and ‘2d’ and the time taken by them to empty the full tank be ‘t’ and ‘T’ minutes respectively.
We also know that the “time taken to fill or empty a tank is inversely proportional to the square of the diameter of the pipe”.
So, t = \(\frac{k}{d^2}\) and T = \(\frac{k}{4d^2}\)
Solving the two, we get
T = \(\frac{t}{4}=\frac{40}{4}\) = 10
So, the two pipes can empty the tank in \(\frac{40 \times 10}{40+10}\) minutes, i.e., 8 minutes

OR
Consider a³ + b³ – a²b – ab² =
= a³ – a² + b³ – ab²
= a² (a – b) – b² (a – b)
= (a – b) (a² – b²)
= (a – b) (a² – b²)
= (a – b)² (a + b) ………………….. (1)
Now, (a – b)² being a square of a real number is either positive or zero, and (a + b) is positive, as a > 0 and b > 0.
So, (a – b)² > 0 (a + b) > 0
By (1), a² + b² + a³ + b³
a³ + b³ > a²b + ab²

Question 27.
Verify that A( B + C) = AB + AC for the matrices [3]
A = \(\left[\begin{array}{ccc}
2 & 0 & -3 \\
1 & 4 & 5
\end{array}\right]\), B = \(\left[\begin{array}{cc}
3 & 1 \\
-1 & 0 \\
4 & 2
\end{array}\right]\), C = \(\left[\begin{array}{cc}
4 & 7 \\
2 & 1 \\
1 & -1
\end{array}\right]\)
OR
If A = \(\left[\begin{array}{lll}
2 & 4 & 0 \\
3 & 9 & 6
\end{array}\right]\) and B = \(\left[\begin{array}{ll}
1 & 4 \\
2 & 8 \\
1 & 3
\end{array}\right]\), then show that (AB)^T = B^TA^T
Solution:
Here,

= \(\left[\begin{array}{ll}
-1 & 13 \\
36 & 17
\end{array}\right]\) …………………. (2)
From (1) and (2), we have A(B + C) = AB + AC

From (1) and (2), we get (AB)^T = B^TA^T

Question 28.
A fertilizer company packs the bags labelled 50 kg and claims that the mean mass of bags is 50 kg with a standard deviation of 1 kg. An inspector points out doubt on its weight and tests 25 bags. As a result, he finds that mean mass is 49. 6 kg. Is the inspector right in his suspicions? ( Given t₂₄ (0.05) = 2.06) [3]
Solution:
Here we have
H₀ : µ = 50, S = 1 and n = 26, \(\bar{X}\) = 49.6
To test H₀, the statistic t is
t = \(\frac{\bar{X}-\mu}{s / \sqrt{n}}=\frac{49.6-50}{1 / \sqrt{25}}\) = -2
⇒ |t| = 2
The table value of t at α =0.05 and 24 d.f is 2.06.
ConcLusion: Since |t| < tα, the inspector is right in his suspicions.

Question 29.
Raman buys a car for which he makes down payment ₹ 1,50,000 and the balance is to be paid in 2 years by monthly instalment of ₹ 25,448 each. If the financer charges interest at the rate of 20% p.a., find the actual price of the car. [3]
[Given (\(\frac{61}{60}\))^-24 = 0.67253]
Solution:
Let P be the amount financed by the financer. Then, the actual price of the car is ₹ (P + 1,50,000)
Given: r = \(\frac{20}{1200}=\frac{1}{60}\) per rupee per month;
n = 2 years = 24 months and EMI = ₹ 25,448
Using “reducing balance method”

= 1526880 × 0.32747 = 500007
So, the financer paid ₹ 500007 and hence the cost of the car is ₹ (5,00,007 + 1,50,000), i.e., ₹ 6,50,007

Question 30.
A person borrowed ₹ 30,00,000 from a bank to purchase a flat and decided to repay the loan by equal monthly instalments in 10 years. If bank charges interest at 9% compounded annually. Determine the EMI by using [3]
(i) flat rate method
(ii) reducing balance method [Given (1.0075)¹²⁰ = 2.4514]
Solution:
Here, P = 30,00,000, r = 9% p.a. = \(\frac{3}{400}\) = 0.0075
per rupee per month, and n = 10 years = 120 months
Using (i) flat rate method,
EMI = P(r + \(\frac{1}{n}\)) = 30,00,000 (\(\frac{3}{400}\) + \(\frac{1}{120}\))
= \(\frac{30,00,000 \times 19}{1200}\) = ₹ 47500
Using (ii) reducing balance method,
EMI = \(\frac{P \times r \times(1+r)^n}{(1+r)^n-1}\)
= ₹ \(\frac{30,00,000 \times 0.0075 \times(1.0075)^{120}}{(1.0075)^{120}-1}\)
= ₹ \(\frac{30,00,000 \times 0.0075 \times 2.4514}{1.4514}\) = 38002.27
Reducing balance method is much more economical than flat rate method.

Question 31.
Solve the following LPP graphically using corner point method: [3]
Maximise Z = x + y
subject to the constraints
x + y ≤ 3; y – 2x ≤ 1; x ≤ 2
x ≥ 0, y ≥ 0
Solution:
Here, the graph of the given constraints and the feasible region, so obtained, is shaded in the graph given below.

Corner point	Corresponding value of Z
O (0, 0)	0 + 0 = 0
A (2, 0)	2 + 0 = 2
B (2, 1)	2 + 1 = 3
C (\(\frac{2}{3}\), \(\frac{7}{3}\))	\(\frac{2}{3}\) + \(\frac{7}{3}\) = 3
D(0, 1)	0 + 1 = 1

Thus, maximum value of Z is 3 which occurs at B(2, 1) and C(\(\frac{2}{3}\), \(\frac{7}{3}\)); and so occurs at every point of the line segment BC.

Section – D (20 Marks)

(All questions are compulsory. In case of internal choice, attempt any one question only)

Question 32.
The demand and supply functions for a commodity are p = x² – 6x + 16 and p = \(\frac{1}{3}\)x² + \(\frac{4}{3}\)x + 4 respectively. Find each of the following assuming x ≤ 5 : [5]
(A) The equilibrium point
(B) C.S. and P.S.at the equilibrium point.
OR
Find \(\int \frac{x^2}{(x-1)^3(x+1)}\) dx
Solution:
(A) We know that the equilibrium point (x₀, p₀) is the point where the demand curve and supply curve intersect. Therefore, the equilibrium is obtained by setting D(x) = S(x)
Now, D(x) = S(x) gives x² – 6x + 16 = \(\frac{1}{3}\) x² + \(\frac{4}{3}\) x + 4
x² – 11x + 18 = 0
(x – 2)(x – 9) = 0 x = 2 or 9
Since x ≤ 5, we take
x₀ = 2
For x₀ = 2, p₀ = (2)² x₀ = 2, p₀ = (2)2 – 6(2) + 16 = 8
The equilibrium point is (2, 8)

Let \(\frac{x^2}{(x-1)^3(x+1)}=\frac{A}{x-1}+\frac{B}{(x-1)^2}\) + \(\frac{C}{(x-1)^3}+\frac{D}{x+1}\) ……………….. (1)
⇒ x² A(x – 1)² (x + 1) + B(x – 1) (x + 1) + C (x + 1) + D (x – 1)³ ………………….. (2)
Putting (x – 1) = 0, i.e., x = 1 in (2), we have
1 = 2C
⇒ C = \(\frac{1}{2}\)
Putting (x + 1) = 0, i.e., x = -1 in (2), we have
1 = -8D
⇒ D = –\(\frac{1}{8}\)
Putting x = 0 in (2), we have 0 = A – B + C – D
⇒ A – B = –\(\frac{5}{8}\)
Putting x = 2 in (2), we have 4 = 3A + 3B + 3C + D
⇒ A + B = \(\frac{7}{8}\)
Now, A – B = –\(\frac{5}{8}\) and A + B = \(\frac{7}{8}\) give
A = \(\frac{1}{8}\), B = \(\frac{3}{4}\)
Putting these values of A. B , C and D in (1), we have

Question 33.
The surface area of a balloon being inflated changes at a constant rate. If initially its radius is 3 units and after 2 seconds it is 5 units, find the radius of the balloon after t seconds. (11.36). [5]
Solution:
Let r be the radius and S be the surface area of the balloon at any time t. Then,
\(\frac{\mathrm{dS}}{\mathrm{dt}}\) = k, where k is constant of proportionality.
⇒ \(\frac{d\left(4 \pi r^2\right)}{d t}\) = k
⇒ 8π\(\frac{d r}{d t}\) = k
⇒ 8πdr = k dt
Integrating both sides, we have \(\int 8 \pi d r=\int k d t\)
4πr² = kt + C ……………. (1)
Initially , r = 3 at t = 0. So , from (1), C = 36π
From (1), we get 4πr² = kt + 36π …………… (2)
Also, r = 5 when t = 2. So, by (2) ,
we have 100 π = 2k + 36π
k = 32π
From (2) ,we have 4πr² = 32πt + 36πr² = 8t + 9
Thus, the radius of the balloon after t seconds will be \(\sqrt{8 t+9}\).

Question 34.
If 1% of the electric bulbs manufactured by a company are defective, find the probabilities that in a sample of 100 bulbs, the number of defective bulbs will be 0, 1, 2, 3,4, 5 respectively. Also, find the probability that (A) 3 or more (B) between 1 and 3, and (C) less than or equal to 2 bulbs will be defective . [5]
(Given e^-1 = 0.368)
OR
In a normal distribution, 7% of the items are under 35 and 89% are under 63. Find the mean and the standard deviation of the distribution.
Solution:
Here, p = 0.01, n = 100.
So, np = λ = 1
P(X = 0) = \(\frac{1^0}{0 !}\) . e^-1
= e^-1 = 0.368
P(X = 1) = \(\frac{1}{1}\) P(X = 0)
= 1 × 0.368 = 0.368
P(X = 2) = \(\frac{1}{2}\) P(X = 1)
= \(\frac{1}{2}\) × 0.368 = 0.184
P(X = 3) = \(\frac{1}{3}\) P(X = 2)
= \(\frac{1}{3}\) × 184 = 0.0613
P(X = 4) = \(\frac{1}{4}\) P(X = 3)
= \(\frac{1}{4}\) × 0.0613 = 0.0153
P(X = 5) = \(\frac{1}{5}\) P(X = 4)
= \(\frac{1}{5}\) × 0.0153 = 0.0031

(A) P(X ≥ 3) = 1 – {P(X = 0) + P(X = 1) + P(X = 2)}
= 1 – {0.368 + 0.368 + 0.184}
= 0.08
(B) P(1 < X < 3) = 1 – {P(X = 1) + P(X = 2) + P(X = 3)} = 0.368 + 0.184 + 0.0613 = 0.6133 (C) P(X ≥ 2) = P(X = 0) + P(X = 1) + P(X = 2) = 0.368 + 0.368 + 0.184 = 0.92

According to the problem, Z = \(\frac{X-2040}{60}\)
(A) P(x > 2150) = P(z > 1.83) = 0.5 – P(0 ≤ z ≤ 1.83)
= 0.5 – 0. 4664, i.e., 0.0336
So, the number of bulbs likely to burn for more than 2150 hours is 2000 × 0.0336
= 67 (Approx.)

(B) P(x < 19050) = P(x < -1.5)
= 0.5 – P(0 ≤ z ≤ 1.5)
= 0.5 – 0. 4332, i.e., 0.0668
So, the number of bulbs likely to burn for less than 1950 hours is 2000 × 0.0668
= 137 (Approx.)

(C) P(1920 < x < 2160)
= P( -2 < z < 2)
= 2 P(0 ≤ x ≤ 2)
= 2 × 0.4772 = 0.9544
So, the number of bulbs Likely to burn for more than 1920 hours but less than 2160 hours is 2000 × 0.9544 = 1909(Approx.)

Question 35.
A bond of face value ₹ 1000 matures in 5 years. Interest is paid semi-annually and bond is priced to yield 8% p.a. If the present value of the bond is ₹ 800, find the annual coupon rate. [Given (1.04)^-10 = 0.6761] [5]
Solution:
Let the coupon rate be r%. We are given the following:
F = Face value of the bond = ₹ 1000
n = number of periodic divident payments = 5 × 2 =10
i = Semi-annual yield rate = 0.04
R = F × i_d = ₹ (1000 × \(\frac{r}{2}\)) = ₹ 500r
Assuming that the bond is redeemed at par, C = Redemption price or Maturity value = Face value = ₹ 1000
Let V be the purchase price of the bond. Then,
V = R\(\left[\frac{1-(1+i)^{-n}}{i}\right]\) + F(1 + i)^-n
= {(500r) \(\left[\frac{1-(1+0.04)^{-10}}{0.04}\right]\) + 1000 (1 + 0.04)^-10}
= {(500r) \(\left[\frac{1-0.6761}{0.04}\right]\) + 1000 × 0.6761}
= ₹ {(500r) [8.0975] + 676.1}
500r = \(\frac{800-676.1}{8.0975}\)
⇒ 500r = 15.30
⇒ r = 0.0306
Hence, the required coupon rate is 3.06%

Section – E (12 marks)

(Alt questions are compulsory. In case of internal choice, attempt any one question only)

Question 36.
Three schools A. B and C organised a mela for collecting funds for helping the rehabilitation of flood victims. They sold hand – made fans, mats and plates from recycled material at a cost of ₹ 25, ₹ 100 and ₹ 50 each. The number of articles sold are given below

School/Article	A	B	C
Hand-fans	40	25	35
Mats	50	40	50
Plates	20	30	40

Based on this information, answer the following questions:
(A) What is the price matrix? [1]
(B) What is the sale matrix? [1]
(C) What is the matrix of funds collected by the.school A?
OR
What is total funds collected by School A, B, C (in order)? [2]
Solution:
(A) \(\left[\begin{array}{c}
25 \\
100 \\
50
\end{array}\right]\)
(B) \(\left[\begin{array}{lll}
40 & 25 & 35 \\
50 & 40 & 50 \\
20 & 30 & 40
\end{array}\right]\)
(C) \(\left[\begin{array}{lll}
40 & 50 & 20
\end{array}\right]\left[\begin{array}{c}
25 \\
100 \\
50
\end{array}\right]\)
OR
₹ 7000, ₹ 6125, ₹7875

Question 37.
The following data shows the percentage of rural, urban and suburban Indians who have a high speed internet connection at home:

Year	Rural	Urban	Suburban
2005	5	8	9
2006	7	10	11
2007	10	14	13
2008	13	20	18
2009	15	22	20

Based on the above data, answer the following questions:
(A) Find a straight line trend by the method of least squares for the rural Indians.
OR
Find a straight line trend by the method of least squares for the urban Indians. [2]
(B) Find a straight line trend by the method of least squares for the suburban Indians is [1]
(C) What is forecast for the year 2010 for urban group, using the trend equation? [1]
Solution:
(A) Here, n = 5(odd).
Let the equation of the straight line of best fit, with the origin at the middle year 2007 and units of x as 1 year, be y = a + bx
By the method of least squares, the values of ‘a’ and ‘b’ are given by
a = \(\frac{\Sigma y}{n}\) and b = \(\frac{\Sigma x y}{\Sigma x^3}\) ………………… (i)

Year	Rural (y)	x	x²	xy
2005	5	-2	4	-10
2006	7	-1	1	-7
2007	10	0	0	0
2008	13	1	1	12
2009	15	2	4	30
	Σy = 50	Σx = 0	Σx² = 50	Σxy = 25

Using (i), we have
a = \(\frac{\Sigma y}{n}\) = \(\frac{50}{5}\) = 10
and b = \(\frac{\Sigma x y}{\Sigma x^3}\) = \(\frac{25}{10}\) = 2.5
Hence, the required equation of the best fitted straight line is y = 10 + 2.5 x

Here, n = 5, Σy = 74, Σx² = 10 and Σxy = 38
So, a = \(\frac{\Sigma y}{n}\) and b = \(\frac{\Sigma x y}{\Sigma x^3}\)= 14.8 and
b = \(\frac{\Sigma x y}{\Sigma x^3}\) = \(\frac{38}{10}\)= 3.8
Hence, the required equation of the best fitted straight line is y = 14.8 + 3.8 x

(B) Here, n = 5, Σy = 71, Σx² = 10 and Σxy = 29
So, a = \(\frac{\Sigma y}{n}\) = \(\frac{71}{5}\) 14.2
and b = \(\frac{\Sigma x y}{\Sigma x^3}\) = \(\frac{29}{10}\) = 2.9
Hence, the required equation of the best fitted straight line is y = 14.2 + 2.9 x

Question 38.
At his usual rowing rate, Ravish can travel 12 miles downstream in a certain river an 6 hours less than it takes to travel the same distance upstream. But if he doubles his usual rowing speed for his 24 mile round trip, the downstream 12 miles would than take only 1 hour less than the upstream 12 miles.
Consider the Ravish’s rowing speed in still water be u km/hr and speed of water current in river be u km/hr.
(A) Form the equation in terms of a and u for first condition ? [1]
(B) What will be the new speed upstream and downstream in second condition? [1]
(C) Find the speed of the water current?
OR
A man can row a boat at 5 km/hr in still water. If the speed of water current in a river is 1 km/hr and it takes him 1 hour to row to a place and come back, how far off is the place? [2]
Solution:
(A) Speed upstream = (u + v) miles/hr
speed downtream = (u + v) miles/hr
Time taken to travel 12 miles downstream
= \(\frac{12}{u+v}\) hr
Time taken to travel 12 miles upstream
= \(\frac{12}{u-v}\) hr
A.T.Q. \(\frac{12}{u-v}\) = -6 = \(\frac{12}{u+v}\)
⇒ \(\frac{12}{u-v}\) – \(\frac{12}{u+v}\) = 6
⇒ \(\frac{24 v}{u^2-v^2}\) = 6
⇒ u² – v² = 4u
⇒ u² = v² + 4v

(B) Time taken to travel 12 miles downstream = \(\frac{12}{2u+v}\)
Time taken to travel 12 miles upstream = \(\frac{12}{2u-v}\)

(C) The equation from (A) is u² = u² + 4v ……………. (1)
From (B)
\(\frac{12}{2u-v}\) – \(\frac{12}{2u-v}\) = 1
⇒ \(\frac{24 v}{4 v^2-v^2}\) = 1
⇒ 4u² – u² = 24v
⇒ 4u² = v² + 24u ……………….. (ii)
From (i) and (ii), we get,
4(v² + 4u) = v² + 24u
⇒ 3v² = 8u
v = \(\frac{8}{3}\) miles/second

OR
Speed of boat in still water = 5 km/hr
Speed of water current = 1 km/hr
Speed downstream = (u + v) = 6 km/hr
Speed upstream = (u – v) = 4 km/hr
Time taken to travel downstream +
Time taken to travel upstream = 1 hour
⇒ \(\frac{x}{6}\) + \(\frac{x}{4}\) = 1
⇒ \(\frac{}{12}\) = 1
⇒x = \(\frac{12}{5}\) = 2.4 km.